【元ヤマハエンジニアから学ぶ】二輪運動力学からライディングを考察！｜回転とGの関係について

二輪工学の専門家、プロフェッサー辻井栄一郎によるライディング考察。バイクのメカニズムや運動力学についてアカデミックに解説し、科学的検証に基づいた、ライテクに役立つ「真実」をお届けします！

TEXT&ILLUSTRATIONS/Prof. Isaac TSUJII

9限目の時に「300km/h超える速度で走行中のMotoGPではマッハ0.5を超えている部分がある」ことを解説させて頂きました。たまにはそんなトリビア的お話をしたいと思います。

今回は加速度にまつわる、ちょっとおもしろいお話です。ぜひバイク談義のネタの一つにしていただけると幸いです。

tips_1：遠心加速度

遠心加速度、単に加速度と言わないこの単語はあまり聞きなれないかもしれませんが、「何G」という数字はご存じかと思います。例えばF1のコーナリングGは約4〜5Gと言われます。重力加速度の何倍あるかを指標とし、1Gは地球の重力と等しく、よく体重と同じとか、2Gで2倍の体重というような表現をされます。また遠心加速度だけでなく、加減速時の加速度も含めて、ご存じのようにGという単位が用いられます。

ちなみに近年のMotoGPでは、コーナリング中に約1.7Gもの遠心加速度が発生しています。条件の良い一般道路を市販のタイヤで走った場合、1Gを超えることはまずありません。レース用のスリックタイヤやF1のダウンフォースの凄さがこれらの数値からも見て取れます。

一方、富士急ハイランドのド・ドドンパ（残念ながら’24年6月末に営業終了を発表）は約3.75GというF1並みの加速度を誰もが体感できました。ちなみに、鍛え上げられた戦闘機パイロットでも約10Gを超えるとブラックアウトして気絶すると言われています。

また、近年ではF1がクラッシュした時やMotoGPライダーが転倒した時の加速度も計測し、公表されています。例えば’24年のF1ハンガリーGP予選での角田裕毅選手のクラッシュは、瞬間的とはいえ68Gもの衝撃だったそうです。これは私の記憶が正しければ、人体の限界に近いGだと思われます。

恐ろしい事に、第二次大戦後のアメリカではジェット戦闘機やロケット開発などの一環で、人は何Gまで耐えられるのか人体実験をしていたそうです。その実験では約60〜70Gで人間の限界と判断したとか。角田選手が無事なのは奇跡とも言えるわけです。

そんなGについて基本的な計算式を改めてですが示しておきます。遠心力は質量mと回転半径rと角速度ωの二乗に比例します。そして、この遠心力を質量で除した（割った）値を、さらに9.8m/s²の重力加速度で除した値が、皆さんもご存じのG（加速度指数）になります。

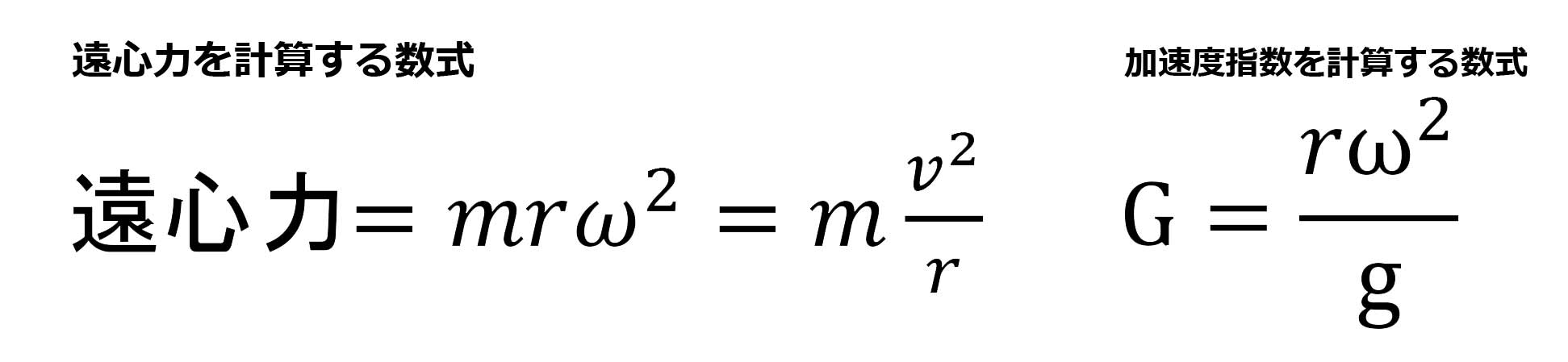
tips_2：コーナリングＧ

例えば鈴鹿サーキットの130Rを走行中のマシンはどうなっているのか計算してみましょう。

実旋回半径にもよりますが、MotoGPの場合1.7Gのコーナリング加速度が発生したとすると200km/h近い速度で通過することになるのですが、この時のコーナリング角速度は約0.3rad/s（ラジアン/秒）です。

急に角速度と言われてもピンとこないかもしれませんが、回転数に換算するとたったの約3rpmに過ぎないのです。

では約4Gのコーナリング加速度を発生するF1の場合はどうなっているのでしょうか。130RをF1はなんと300km/h以上で駆け抜けていきます。4Gも出るはずです。

コーナリング角速度は約0.48rad/sで、回転数に換算するとMotoGPよりも速いのですが、それでも約4.6rpm程度です。

tips_3：ホイールの加速度（Ｇ）

マシンには回転しているものがたくさんあります。回転体には当然遠心力が発生し、加速度・Gがかかります。回転しているのが見える物の代表がホイール（タイヤ）です。

では、タイヤ単体の加速度はいったい何Gなのでしょう？

17インチホイールでは、タイヤの外径はだいたい600mmになり、スーパースポーツは300km/h、MotoGPでは360km/hを超えます。340km/hを超えるとタイヤの回転数は3000rpmを超えます。130Rを駆け抜けるF1のコーナリング回転数の比ではありません。

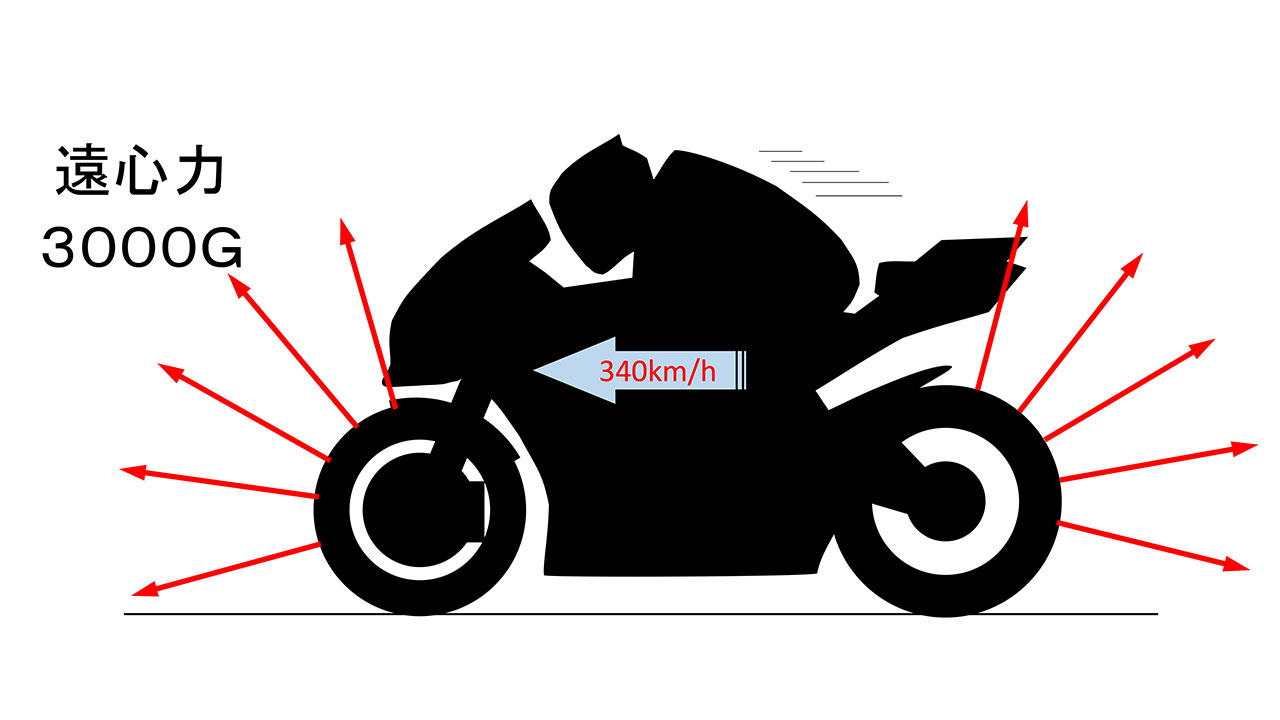
この時の遠心加速度は、なんと3000Gを超えてしまうのです。ゼロの数は間違っていません（笑）。

最高速度400km/hを超えるブガッティ・トゥールビヨン（旧ベイロン）のユーザーマニュアルにはなんと「最高速度を出す時は、タイヤとホイールは新品に交換してから」と記載されているそうです。

その時のタイヤには3600Gを超える遠心力が発生するので、安全のためにはやむを得ません。

’70年代のF1のタイヤはラジアルではなくまだバイアスタイヤが一般的でした。サイドウォール剛性がラジアルほど無かったバイアスタイヤは遠心力で外径が大きく膨らみ、直線ではマシンの車高が数10mmも高くなっていました。

さらには、過去にMotoGPでは直線でタイヤがバーストしたり、F1ではタイヤ問題で某メーカーのタイヤを履くチームはレースをボイコットしたことがあります。それらはタイヤには巨大な遠心力が発生している証と言えます。

300km/hを超える速度でタイヤがバーストすると危険なことは誰にでも分かりますが、バーストしたタイヤの破片がたった50gだったとしても、その質量×3000Gなので150kgfを超える力で飛び出していく事になります。柔らかいゴムでも、もはや弾丸です。

300km/h以上で走行するというのは、実のところかなり命がけなんですよ。エンジニアの私はそんな事を考えながらテストコースのストレートを300km/hオーバーで駆け抜けていました。

tips_4：エンジンのＧ

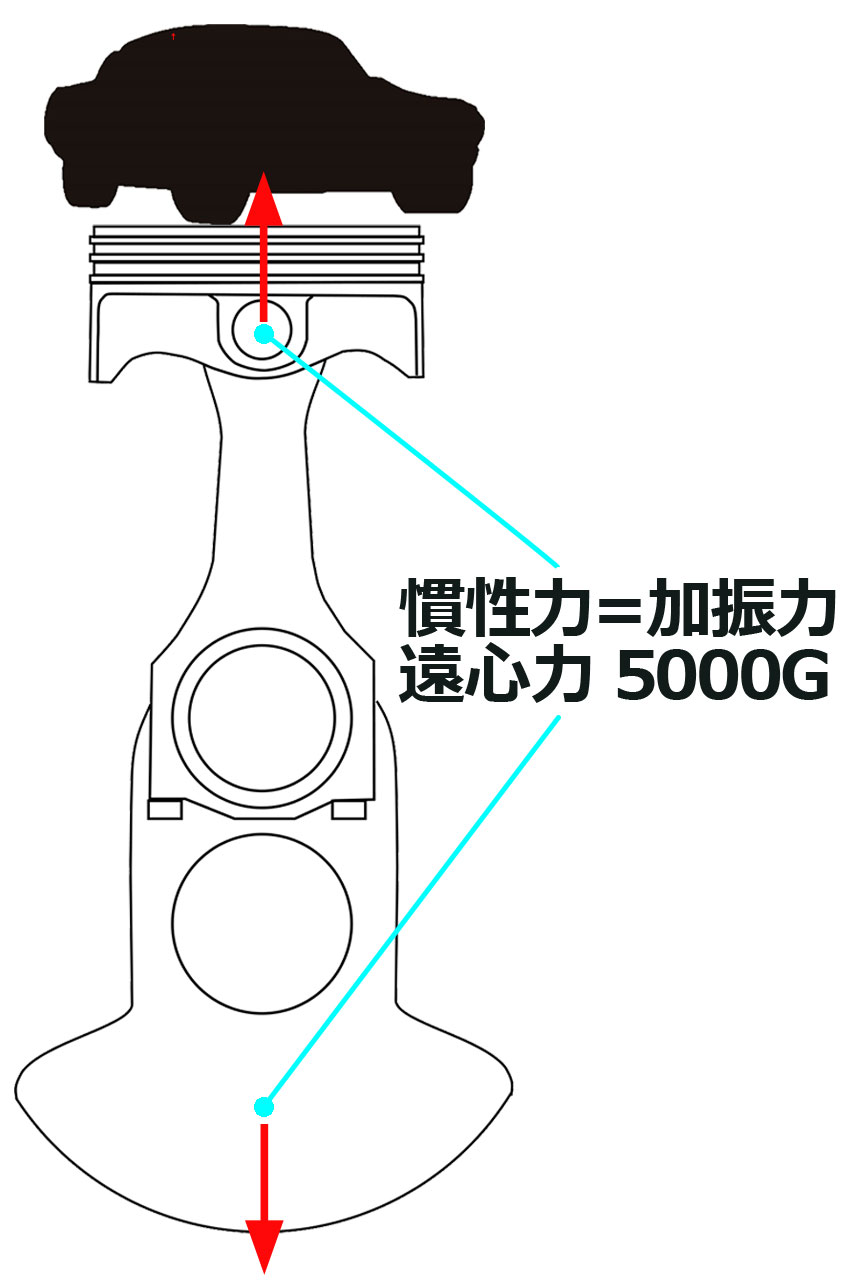
エンジンも回転しています。例えばヤマハのYZF-R1の場合、エンジンは最大馬力時にはご存じのように13500rpmで回ります。クランクシャフトの回転半径はストロークの半分なので25.45mmです。その時の遠心加速度はなんと5,000Gを超えてしまいます。

そしてその時の遠心力、この場合我々エンジニアは加振力と呼びますが、なんと約1.7トンになってしまいます。単位がトンのオーダーです。

1.7トンというと乗用車なみの重さです。4気筒のR1には乗用車4台分の荷重がクランクシャフトとピストンでは発生しているのです。その荷重に耐えるだけの強度がエンジンには求められるのです。

ちなみに15000rpmにもなるF1のエンジンでは、なんと6000Gを超える遠心加速度が発生し、加振力は私の推定ですが、約2.5トンにもなっていると思われます。タイヤ開発もエンジン開発も、エンジニアの努力と技術力が問われているわけです。